Basic HTML Version
Ha a háromszög egyenlő szárú , akkor a háromszögnek van szimmetriatengelye .
Ha a háromszögnek van szimmetriatengelye , akkor a háromszög egyenlő szárú .
3. példa
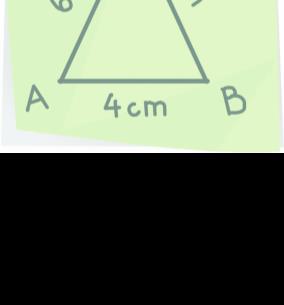
Szerkesszünk egyenlő szárú háromszöget, amelynek oldalai 4 cm és 6 cm hosszúak!
Megoldás
Vázlat
Két eset lehetséges:
I.
A háromszög alapja 4 cm,
szára 6 cm hosszú.
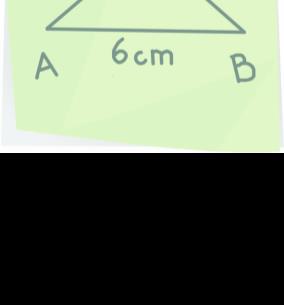
II.
A háromszög alapja 6 cm,
szára 4 cm hosszú.
Megrajzoltuk a háromszögeket, min
ha már megszerkesztettük volna
feladatot.
Az ilyen rajzot
vázlatrajznak
neve
zük. Az adatokat is feltüntetjük a ra
zon.
B
A
C
1
C
2
Összefüggések
I.
A háromszög
C
csúcsa az
A
és
B
csúcsoktól 6 cm távolság-
ra van, tehát rajta van az
A
pont köré írt 6 cm sugarú körön,
és rajta van a
B
pont köré írt 6 cm sugarú körön, azaz rajta
van e két kör metszéspontján.
A szerkesztés lépései
1. Megszerkesztjük a 4 cm hosszúságú szakaszt. (A szakasz két
végpontja a háromszög
A
és
B
csúcsa.)
2.
A
középpontú, 6 cm sugarú kört szerkesztünk. (Elég a kör
C
metszésponthoz közeli pontjait megrajzolni.)
3.
B
középpontú, 6 cm sugarú kört szerkesztünk. (Elég a kör
C
metszésponthoz közeli pontjait megrajzolni.)
4. Megjelöljük a két kör metszéspontjait (
C
1
,
C
2
).
5. Összekötjük az
A
,
B
,
C
1
és az
A
,
B
,
C
2
pontokat.
Ellenőrzés
Az így szerkesztett
C
pont rajta van az
AB
szakasz felezőmerő-
legesén, a megszerkesztett háromszög egyenlő szárú.
Két ugyanolyan háromszöget kaptunk. Az
AB
szakaszt a síkon
bárhol felvehetjük, akkor is az előzőekkel azonos háromszöget
kapunk. Ezek a háromszögek kölcsönösen fedésbe hozhatók egy-
mással.
138

