Basic HTML Version


Egyenletek és egyenlőtlenségek megoldása mérlegelvvel,
szöveges feladatok
(Kiegészítő tananyag)
1. példa
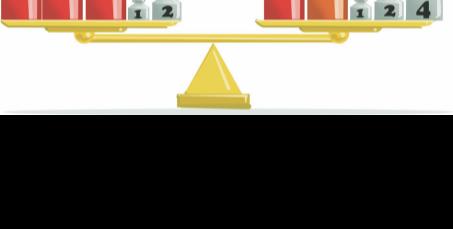
A mérlegen lévő mérőtömegekre csak a mérőszámukat írtuk rá, mindegyik mértékegysége kg.
Hány kilogramm egy befőtt tömege, ha minden
befőtt tömege azonos?
Milyen nehéz lehet egy bőrönd, ha minden b
rönd tömege azonos?
Megoldás
Ha mindkét oldalról 2-2 üveg befőttet leve-
szünk, akkor
2 üveg tömege + 3 kg = 7 kg.
Ha mindkét oldalról leveszünk 3 kg-ot, akkor
2 üveg tömege = 4 kg.
Ha mindkét oldal felét vesszük, akkor
1 üveg tömege = 2 kg.
Nézzük meg, jó lesz-e!
A bal oldali serpenyőben lévő mérőtömegek és
üvegek tömege összesen 11 kg, és ugyanennyi a
jobb oldaliban lévőké is.
Ha mindkét oldalról leveszünk két bőröndöt, a
kor
26 kg 1 bőrönd tömege + 6 kg.
Ha mindkét oldalról leveszünk 6 kg-ot, akkor
20 kg 1 bőrönd tömege.
Elmondhatjuk, hogy 1 bőrönd tömege 0 és 20 k
közé esik.
Az eredményünket ellenőrizve azt kapjuk, hog
ha 20 kg-os lenne egy bőrönd, akkor egyensúl
lenne, ha ennél kisebb, akkor a mérleg állás
olyan, mint a rajzon.
A megoldások során csak úgy változtattuk a mérlegek mindkét oldalát, hogy azok állása ne válto
zon.
Tapasztalataink szerint
az egyenlőség nem borul fel,
ha
•
az egyenlet mindkét oldalán álló kifejezést ugyanannyival növeljük vagy csökkentjük;
•
az egyenlet mindkét oldalán álló kifejezésnek ugyanannyiszorosát vagy ugyanannyiad rész
vesszük.
Ha az egyenletek megoldásában ezt a törvényszerűséget használjuk fel, akkor
mérlegelvvel
oldju
meg a feladatot.
Amelyik feladat lebontogatással megoldható, az mérlegelvvel is, de fordítva már nem igaz.
2. példa
Ha az egyenlet mindkét oldalán szerepel ismeretlen, akkor mérlegelvvel célszerű megoldani azt.
Hány könyv van egy csomagban? Írjunk az ábrákról egy-egy egyenletet!
210

